Clases de Octubre


28 de septiembre del 2015 

Vectores y Geometria Analitica en el Espacio 

Funciones Implícitas

  • R2 F(X,Y) = 0 Función implícita de dos variables, existen 2 posibles funciones:
  1. x(y) ---- x = f(y)
  2. y(x) ---- y = g(x)


Sistema de Funciones Implícitas 


f (x,y) = 0
g (x,y) = 0

Representa una intersección de las curvas 2 o más puntos.

·         R3 F(X,Y,Z) = 0       Función implícita de 3 variables
x = f(y,z) --- x: valor dependiente;  y,z: variables independientes.
y = g(x,z) --- y: valor dependiente; x,z variables independientes.
z = h(x,y) --- z: valor dependiente; x,y: variables independientes.
 
Geométricamente las funciones implícitas representan una superficie en el espacio.

Casos Particulares

f(x,y) = 0  Superficie cilíndrica de generatriz paralela al eje oz
g(x,y) = 0  Superficie cilíndrica de generatriz paralela al eje oy
h(x,y) = 0  Superficie cilíndrica de generatriz paralela al eje ox
1 de octubre del 2015

Ecuación de la Recta en el Espacio

  • Dado un punto y el vector director de la recta 

Una recta en el espacio queda determinada por un punto de ella A ( x1, y1, z1)   y un vector director  u→ = ( a, b, c)


Ecuaciones de la recta

Ejemplos 

  • Dado dos Puntos



5 de octubre del 2015

Ecuaciones del Plano en el Espacio

  • Ecuación del plano dado un punto y el vector normal del plano
Ecuación vectorial

Un plano queda determinado por un punto P y un par de vectores con distinta dirección.
Para que el punto P pertenezca al plano π el vector vector tiene que ser coplanario con vector u y .
ecuación vectorial del plano
igualdadecuación vectorial del planoecuación vectorial de plano
Ecuación general o implícita del plano
Un punto está en el plano π si tiene solución el sistema:sistema
Este sistema tiene que ser compatible determinado en las incógnitas λ y µ· Por tanto el determinante de la matriz ampliada del sistema con la columna de los términos independientes tiene que ser igual a cero.Ecuación general del plano
Desarrollamos el determinante.operaciones
Damos los valores:
coeficientes
Sustituimos:
ecuación
Realizamos las operaciones y le damos a D el valor:
ecuación
Obtenemos la ecuación general de plano:
eco general del plano
Ecuación canónica o segmentaria del planoecuación canónica en el espacio

 Sean los puntos A(a, 0, 0), B(0, b, 0) y C(0, 0, c), la ecuación canónica viene dada por:
ecuación canónica de la recta en el espacio
coeficientes

Ejemplo

Hallar las ecuaciones paramétricas e implícitas del plano que pasa por el punto A(1, 1, 1) y tiene como vectores directores a vector y vector.
ecuaciones paramétricas
ecuación generalecuación general

9 de  octubre del 2015

Intersección de planos, distancia de un punto a un plano, ángulo entre planos


INTERSECCIÓN DE PLANOS.


Dos planos se intersectan en una línea recta ( salvo que ellos sean paralelos, caso en el cual la intersección es $\emptyset$ ). Teniendo sus ecuaciones cartesianas se trata entonces de resolver un sistema de dos ecuaciones con tres variables, para encontrar puntos en la intersección. 
Ejemplo 1: Encontar la intersección de los planos $2x-3y+z=4$ y $-5x+2y-5z=-2$
Se resuelve el sistema cuya matriz aumentada es MATH cuya forma escalonada
reducida es MATH . La solución del sistema es MATH
Podríamos ahora darle 2 valores a $z$ para obtener dos puntos sobre la recta y obtener así el vector director. Pero si sabemos que $z$ puede tomar cualquier valor, haciendo $z=t$ se obtiene
MATH que son las ecuaciones paramétricas de la recta de intersección.
El vector director de esta recta es MATH ( o si se quiere $( 13,5,-11) $) Un punto sobre la recta es MATH


DISTANCIA DE UN PUNTO A UN PLANO. 

Se quiere encontrar la distancia del punto MATH al plano de ecuación $ax+by+cz=d$  Para encontrar esta distancia sea MATH un punto del plano. 
Por lo tanto MATH
cosMATH además MATH, simplificando: MATHComo una distancia es una cantidad positiva y el numerador podría dar negativo se toma valor absoluto

Distancia de un punto MATH al plano $ax+by+cz=d$ es MATH 

Ejemplo 2: Encontrar la distancia del punto $( 2,-4,7) $ al plano de ecuación $-x+y-3z=6$ 

Ya no hay que deducir la fórmula; al utilizar el resultado, MATH


Ángulo entre dos Planos

El ángulo formado por dos planos es igual al ángulo agudo determinado por los vectores normales de dichos planos.vectores directoresfórmula

Dos planos son perpendiculares si vectores directores son ortogonales.planos perpendiculares

Haz de Planos

haz de planos

Si r viene definida por sus ecuaciones implícitas:ecuaciones implícitas
la ecuación del haz de planos de eje r viene dada por la igualdad:haz de planos
Si dividimos por λ y hacemos k, la ecuación del haz resulta:ecuación del haz
12 de octubre del 2015

Distancia de un Punto en un Plano

La distancia de un punto, P, a un plano, π, es la menor de la distancia desde el punto a los infinitos puntos del plano.
Esta distancia corresponde a la perpendicular trazada desde el punto al plano.
determinación punto plano
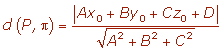
distancia punto plano
Ejemplo
Hallar la distancia del punto P(3, 1, −2) a los planos ecuación del plano y ecuación del plano.
distancia
distancia
Hallar la distancia del punto Q(5, 5, 3) al plano ecuación del plano.
ecuación del planodistancia
15 de octubre de 2015 

Ecuación Vectorial de la Esfera 

 Ecuación de la esfera (centrada en el origen O):
  x2 + y2 + z2 = R2
  siendo R el radio de la esfera centrada en el origen.


Ecuación de la esfera centrada en un punto P(a,b,c):
(x-a)2 + (y-b)2 + (z-c)2 = R2   

Ejemplo



19 de octubre del 2015

Cilindro y Superficies Cuádricas

Cilindro

Ecuación de la superficie cónica:
  x2 + y2 = R2       (superficie cilíndrica de revolución; las secciones transversales al eje z son circulares)
*   *   *
     (superficie cilindroide; las secciones transversales al eje z son elipses -de semiejes a, b-)


Cuádricas

Análisis de Gráficos de la Superficie 
Para realizar un análisis de superficies en R3 se debe realizar : 
  1.   Intersección con los eje coordenados
  • con el eje ox
  • con el eje oy
  • con el eje oz
2.  Intersección con los planos coordenados 
  • con el plano xoy
  • con el plano xoz
  • con el plano yoz 
3. Intersección con planos paralelos a los planos coordenado
  • con el plano paralelo al plano xoy
  • con el plano paralelo al plano xoz
  • con el plano paralelo al plano yoz

Ejemplo

Realice el análisis gráfico de X^2 + Y^2 = Z

  1.   Intersección con los eje coordenados
  2.  Intersección con los planos coordenados 
  3.  Intersección con planos paralelos a los planos coordenado


22 de octubre del 2015

Función Vectorial de la Variable Real

Una función es una regla que asigna a cada elemento del dominio un elemento del rango. Una función vectorial es una función cuyo dominio es un conjunto de números reales y cuyo rango es un conjunto de vectores. 

DOMINIO: El dominio de una función vectorial esta dado por la intersección de los dominios de cada una de las funciones componentes.

OPERACIONES: 
  • Suma:  (f+g)(t) = [ f1(t) + g1(t)]; [f2(t) + g2(t)];........; [fn(t) + gn(t)]
  • Producto de una función por un escalar: a.f(t) = a.f1(t); af2(t);........; a.fn(t)
  • Producto de funciones : < f(t)/g(t) > = f1(t).g1(t) + f2(t).g2(t) + ......... + fn(t).gn(t)
  • El modulo del vector es igual a la raíz cuadrada de cada uno de sus componentes elevados al cuadrado
  • Composición de funciones: (foh)(t) ssi f es función vectorial y g es función real

Ejemplos:

$(1)$ $f(t)=(t^2,t+1)$ es continua en todo $\mathbb{R}$ ya que $f_1(t)=t^2$ y $f_2(t)=t+1$ lo son.
$(2)$ ${\displaystyle g(t)=(\sqrt{t},\frac{ \mbox{ sen }t}{t}) }$ si $t\neq 0$ y $g(0)=(0,0)$.

\begin{displaymath}g_1(t)=\cases{\displaystyle{\sqrt{t}, t\neq 0}&\cr 0 , t=0&}=... ...\frac{ \mbox{ sen }t}{t}, t\neq 0}&\cr&\cr \quad 0 ,\quad t=0&}\end{displaymath}
$g$ es continua en $\mathbb{R}^*$, pero no en $t=0$ ya que 
\begin{displaymath}\lim_{t\to 0}g(t)=(0,1)\neq g(0)\end{displaymath}
Fijémonos que $g_2$ no es continua en $0$.
$(3)$ ${\displaystyle h(x)=(\frac{x^2-1}{x-1},\frac{ \mbox{ sen }(x^2-1)}{x^2-1}) }$ si $x\neq 1$, $x\neq 1$; $h(1)=(2,1,2)$, $h(-1)=(0,0,0)$.
$h_1$ es continua en todo $\mathbb{R}$ y $h_3$ también, pero $h_2$ no es continua en $x=-1$ ya que 
\begin{displaymath}\lim_{x\to -1}\frac{x^2-1}{x-1}=1\neq 0=h_2(-1)\end{displaymath}

26 de octubre del 2015

 Derivación

Integración
29 de octubre del 2015

LONGITUD DE CURVA Y ARCO

La longitud de una curva plana con representación paramétrica; x=f(t), y=g(t), a<=t<=b, se define como el límite de las longitudes de polígonos inscritos y en el caso donde f' y g' son continuas:


Longitud de Arco Curva Plana


Para el caso de una curva en el espacio se define de una manera similar, siendo
F(t)=(f(t),g(t),h(t))
a<=t<=b, donde f',g' y h' son continuas

Longitud de Arco Curva en 3D
Forma General



Función de la Longitud de Arco
Ejemplo
Determine la longitud de arco de la curva y=(x/2)2/3 de [0,2]

Triedro Movil

Sea C una curva alabeada:
r(t) = f1(t)i + f2(t)j + f3(t)k






cada par de vectores forman un plano:
PLANO OSCULADOR: T ^ N
PLANO NORMAL: N ^ B
PLANO RECTIFICANTE: T ^ B

Vector Binormal: r'(t) x r''(t) = B
Vector Normal : B x T

 EC. PLANO OSCULADOR (PO):  B1(X - Xo) + B2(Y - Yo) + B3(Z - Zo) = 0

EC. PLANO NORMAL (PNP):  T1(X - Xo) + T2(Y - Yo) + T3(Z - Zo) = 0

EC. PLANO RECTIFICADOR (PR): N1(X - Xo) + N2(Y - Yo) + N3(Z - Zo) = 0

EC. RECTA TANGENTE (RT):  (X - Xo)/T1 = (Y - Yo)/T2 = (Z - Zo)/T3

EC. RECTA BINORMAL (RB):  (X - Xo)/ B1 = (Y - Yo)/ B2 = (Z - Zo)/ B3

EC. RECTA NORMAL PRINCIPAL (RNP):  (X - Xo)/ N1 = (Y - Yo)/ N2 = (Z - Zo)/ N3

Como podemos ver en la imagen el Plano Normal es perpendicular al Vector Tangente, el Plano Rectificante es perpendicular al Vector Normal Principal y el Plano Osculador es normal al Vector Binormal. Sus expresiones son:
Plano Normal.
(X−r(t))∗T=0
Plano Rectificante
(X−r(t))∗N=0
Plano Osculador.
(X−r(t))∗B=0


Bibliografía:

  • http://matcalculus.wikidot.com/frenet
  • http://www.calculointegrales.com/p/longiutd.html
  • http://www.slideshare.net/zq0/integrales-en-funciones-vectoriales
  • http://www.ehu.eus/juancarlos.gorostizaga/apoyo/geometr2.htm
  • http://www.vadenumeros.es/segundo/ecuaciones-de-la-recta.htm
  • http://www.vitutor.com/analitica/recta/ecuaciones_plano.html
Publicado por en
Etiquetas:

No hay comentarios:

Publicar un comentario

Suscribirse a: Enviar comentarios (Atom)